pythonでベイジアンA/Bテスト(RCT)を行ってみた

最近はベイズが流行っているので自分もベイズを齧ろうと、冬休みにA/Bテストをpythonで行ってみました。 使用したのはpymc3です。事前知識は、信用区間は信頼区間と違って解釈がし易いよ！、A/Bテスト（RCT）ってこんなことをやってるよ！くらいを想定しています。
ちなみに個人的にはA/Bテストっていう言葉よりRCTという言葉のほうが好みです。

参考資料

参考資料は以下の通りです。

Pythonで体験するベイズ推論 PyMCによるMCMC入門

キャメロン本と呼んでいる本で、コードで何をしているのかわかりやすく書いてある、訳注もわかりやすいのでおすすめです。 ちなみに訳者の玉木さんがUdemyで行っているベイズ推定とグラフィカルモデルもわかりやすいのでおすすめです。

ベイズ統計モデリング: R,JAGS, Stanによるチュートリアル 原著第2版

犬の表紙が可愛い枕の様な本、犬ベイズと呼んでます。私はRをあまり使いませんが、手を動かす時に気になるポイントがまとまっていて重宝します。

岩波データサイエンス Vol.1

前掲のキャメロン本はpymc3の前のver.のpymcなので、この本の岩波DS vol.1のpymc3解説記事とキャメロン本のweb版にあるpymc3対応コードを参照しました。

A/Bテスト

テストデータの作成

まず初めに必要なもののインポートとサンプルデータの生成を行いましょう。
実行環境はjupyter notebookです。

from numpy.random import *
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
import pymc3 as pm

# データ生成関数
def gen_sample(p, size):
    """
    Sample generating funcion
    """
    sample = binomial(n=1, p=p, size=size)
    commited = sum(sample)
    num = len(sample)
    rate = commited/num
    print("""
    CV数：{}
    サンプルサイズ：{}
    CV率：{}
    """.format(commited, num, rate))
    return sample

gen_sample()関数はパラメータpのベルヌーイ分布から、size個サンプリングする関数です。ここでpは観測できない真のパラメータに相当します。 我々が知りたいのはControl group（対照群、統制群）とTreatment group（介入群、処置群）の２群の真のパラメータ：p、の差なので対照群と介入群に相当するデータをそれぞれ生成しましょう。 今回は会員10万からランダムに9万人に施策を行った結果、施策を行った9万人（treatment group）のCV率は2%上昇したとするデータを作ります。 勿論、この2%という数字は実際には判らない、A/Bテストで推定したい数字になります。

control_p, treated_p = 0.15, 0.17
print('対照群')
controlled = gen_sample(control_p, 10000)
print('介入群')
treated = gen_sample(treated_p, 90000)

今回観測（生成された）された対照群と介入群のCV率は0.1487と0.1592でした。我々の目的は介入群と対照群それぞれの真のCV率、の推定量を得て、その差を評価することです。

頻度主義（通常のA/Bテスト）的にはをの関数と見做して、（これを尤度（関数）と呼ぶ）を最大にするをの最尤推定量と呼び、その名の通りの推定量となります（これはCV率の標本平均と一致します）。なので対照群と介入群のCV率に対して２群の比率の差の検定を行い、有意差があればだけの効果が施策にはあったと見做します。

頻度主義では真のθが1つ存在すると考えるので上述のもスカラーでした。しかしベイジアンはのを確率変数と見做してその分布、 $$ \begin{align} p(\theta | x) = \frac{p(x | \theta)p(\theta)}{p(x)} \propto p(x | \theta)p(\theta) \end{align} $$ を求めます。今回の例で使うMCMCは数値計算によってこれを求めます。
ここではθの事前分布で、は尤度です。最尤推定とは尤度という言葉が指すものが見かけ上違うので注意してください。
今回、θの事前分布が判らない（＝CV率がどれ位か、ということが事前に判らない）という想定のもとで無情報事前分布（[0, 1]区間の一様分布）を採用します。つまり、ある個人がCVするかどうかが以下の様に決まるモデルを考えます。

$$ \begin{align} t &\in \{ Treatment, Control \} \\ \theta_t &\sim Uniform(0, 1) \\ x_t &\sim Binom(\theta_t) \end{align} $$

MCMCによるパラメータ推定とその結果

それではモデルを構築していきます。
ほぼキャメロン本のweb版そのままです。

with pm.Model() as model:
    # 事前分布を対照群と介入群それぞれに設定
    theta_t = pm.Uniform("theta_t", 0, 1)
    theta_c = pm.Uniform("theta_c", 0, 1)
    
    # 対照群と介入群のθの差を定義
    # 我々の目的はこのdeltaの分布の形状を知ること
    delta = pm.Deterministic("delta", theta_t - theta_c)
    
    # 観測値をベルヌーイ分布にセット
    obs_t = pm.Bernoulli("obs_t", theta_t, observed=treated)
    obs_c = pm.Bernoulli("obs_c", theta_c, observed=controlled)

    # サンプリングを実行
    step = pm.Metropolis()
    trace = pm.sample(30000, step=step, njobs=2)
    burned_trace=trace[1000:]

さて、これで事後分布からサンプリングが終了しましたのでプロットしてみましょう。

# サンプリング結果を変数に格納
theta_t_samples = burned_trace["theta_t"]
theta_c_samples = burned_trace["theta_c"]
delta_samples = burned_trace["delta"]

# 対照群と介入群のθの事後分布をプロット
plt.figure(figsize=(15, 6))
plt.title("Posterior distribution of Treated and Controlled")
plt.vlines(treated_p, 0, 50, linestyle="--", label="true $theta_t$ (unknown)")
plt.vlines(control_p, 0, 50, linestyle="--", label="true $theta_c$ (unknown)")
plt.hist(theta_t_samples, bins=50, histtype="stepfilled", normed=True, alpha=0.5)
plt.hist(theta_c_samples, bins=50, histtype="stepfilled", normed=True, alpha=0.5)
plt.legend()
plt.show()

# 対照群と介入群のθの差の事後分布をプロット
CI = pm.stats.hpd(delta_samples, alpha=0.01)
plt.figure(figsize=(18, 8))
plt.title("Posterior distribution of delta")
plt.vlines(np.median(delta_samples), 0, 50, linestyle="-", label="Median")
plt.vlines(CI[0], 0, 50, linestyle="--", label="99% CI")
plt.vlines(CI[1], 0, 50, linestyle="--")
plt.hist(delta_samples, bins=50, histtype="stepfilled", normed=True, alpha=0.5)
plt.legend()
plt.show()

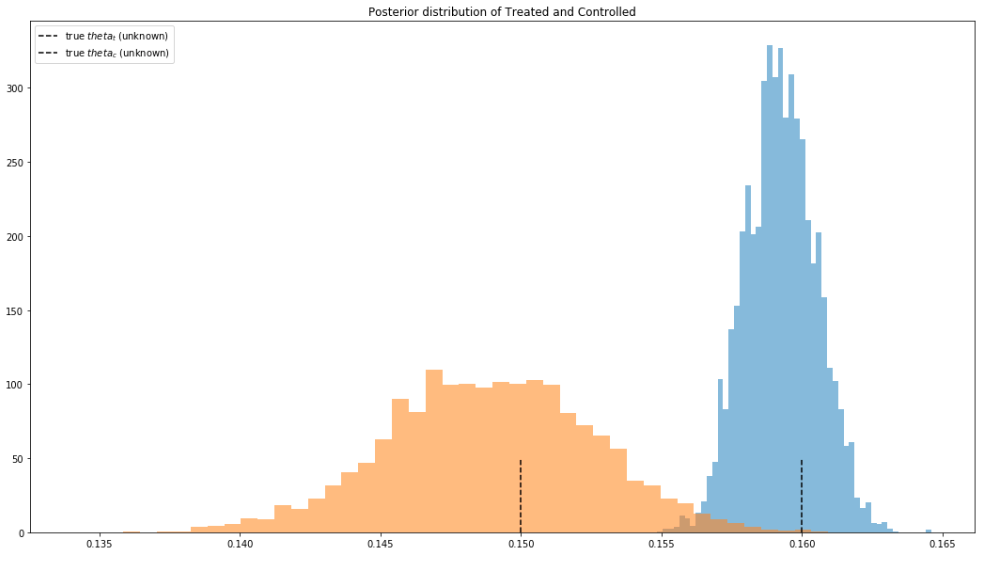
対照群と介入群のθの事後分布のプロット（図１）
破線は真の値を示す

対照群と介入群のθの差(delta)の事後分布のプロット（図２）
実線は中央値、破線は99%信用区間を示す。 中央値は0.0104。

さて、これで欲しいパラメータの事後分布が手に入りましたので考察をします。

結果の考察

先ず、図２を見てみましょう。図２は対照群と介入群同士のθの差の事後分布をプロットしたものです。 今回興味があるのは介入群のCV率が対照群のCV率より高いかなので、deltaが0より大きい確率を計算してみます。

print((delta_samples>0).sum()/len(delta_samples))
>> 0.997

この結果より、99.7%以上の確率で対照群と介入群のθには有意に差があり、その差deltaの中央値より施策の効果の大きさは0.01%程度（相対値ではないことに注意）だということがわかりました。*1 図１のオレンジ色の対照群と青色の介入群の分布に殆ど重なりがないことからも、対照群と介入群のθには差があることが見て取れます。 (今回は、介入群のCV率＞対照群のCV率、に興味があったので上のような計算を行いましたが、両側検定を行うのであれば9n%信用区間 - 9n％の確率で真の値がある範囲 - に0が含まれてるかを見てください。)

また対照群の分布の分散が大きいことから、追加的なサンプルが取得できるなら対照群のサンプルを増やすことで推定の精度を向上させられることがわかります。今回は幸運にも99.7%以上という高い確率でCV率：θに差があることが分かりましたが、これが80％の様な低い確率であったならばサンプルを（実験のデザインに収まる範囲で） 増やす、という判断が下せます。これがベイジアンのいいとこだと私は思います。

点推定を求められたら

さて、ここまでの結果を上司に見せたところ、あなたはこう言われるかもしれません、「分布というのはよくわからないのでA/BテストのでどれだけCV率が上がったかが判る数字を１つ持って来い」、と。 この様に点推定値を求められた場合、キャメロン本では事後分布の平均値や中央値よりも下側50パーセンタイル以下の値を報告することを勧めています。 保守的になるならそのほうが良いのかもしれませんが、説明を求められた時の説明のし易さや、中央値が機能しないほど変な形の分布に為ることはそんなに無いと思われることから私自身は基本的に中央値を報告すればでいいのではないかなと思います。

検定力（サンプルサイズ)について

注）以下の議論は文献を引いていないので、修正する可能性があります。

今回は1%という小さな差を検出することに成功しましたが、果たしてこれはたまたまなのでしょうか、それとも今回のサンプルサイズなら1%の差はわけもなく検出できる差なのでしょうか。ベイジアンにサンプルサイズという考えはそぐわない気もしますが、実用上は頻度主義で言う所の検定力が気になります。そこで真の差と、対照群・介入群それぞれのサンプルサイズを固定した上で今回のシミュレーションを2000回実行し、deltaの事後分布が0より大きい確率をヒストグラムにしたのが下のプロットになります。

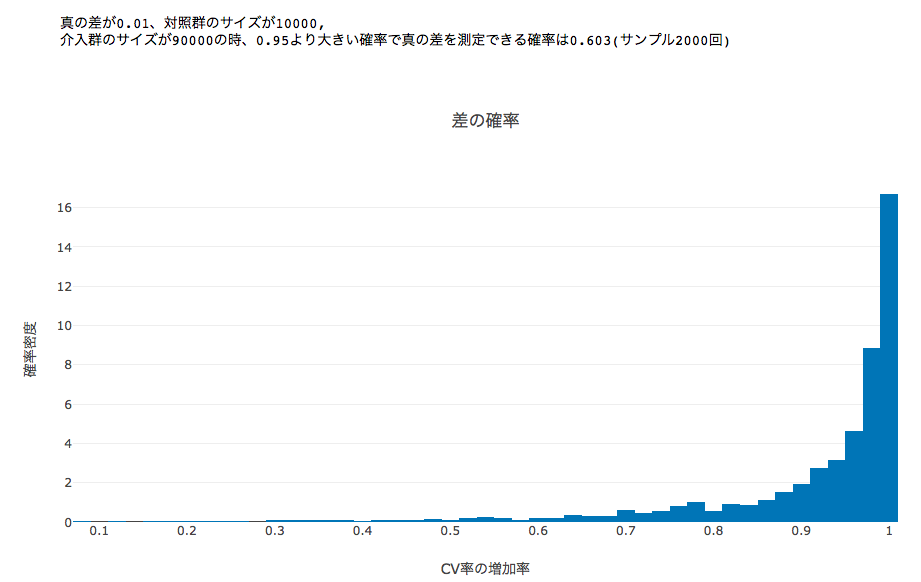画像中にprintされているように閾値を0.95に設定した（=の時、施策に効果があったと）時、今回のサンプルサイズでは検出力は6割程でした。

そこで真の差を2%に変更して同じシミュレーションを回すと今度は以下のように0.98以上の確率でθの差を正しく検出できました。
このことから「施策には2%以上の差があると仮定」すれば今回の設定でA/Bテストを行って良いといえるでしょう。施策には2%未満の効果しか無いなら検出できなくても良いということですね。このあたりは頻度主義の効果量の考え方と同じに為ると思います。

よくわからない所

• informativeな事前分布を使うことで検定力を改善できる気はしますがあまり良くわかっていません。
• 今回の設定だと、CV率の真の分布は確率1の定数、と見做していますがこれが正しいのかよく判りません。例えば犬ベイズ本のp.378では検定力分析に際してパラメータを仮説分布からランダムに取ってくる例を出していますが、今回の設定だと対照群も介入群も事前知識がないのでパラメータの仮説分布が[0, 1]の一様分布になります。この時に犬ベイズ本と同様のことを実行して意味があるのか判りません。しかし真の分布を確立1の定数と見做すのもベイズっぽくなくて悩んでいます。

終わりに

今回はA/Bテストをベイジアンの観点から行いました。 実際には共役事前分布*2を使えばMCMCを使わずとも早く計算を行えるのですが、今回はpymc3の練習も兼ねてMCMCを使いました。共役事前分布を使う方法は今度追記しようと思います。

*1:ベイジアンでも有意という言葉を使うらしい

*2:「きょうえき」と読むと思っていたら「きょうやく」と読む人もいるらしい